円筒ハニカムコア構造とは?
六角形セルが円周方向に並ぶ「円筒ハニカムコア構造」。
セルの向きが半径方向に揃うため、回転体や円筒シェルでラジアル荷重を支えやすいのが特徴。
目次
1. 設計変数
独立な設計変数は次の4つ。
- l:外周セル(正六角形)の一辺
- h:コア高さ(等脚台形の高さ)
- t:コア壁厚さ(シート厚)
- θ:等脚台形の頂角(離散値)
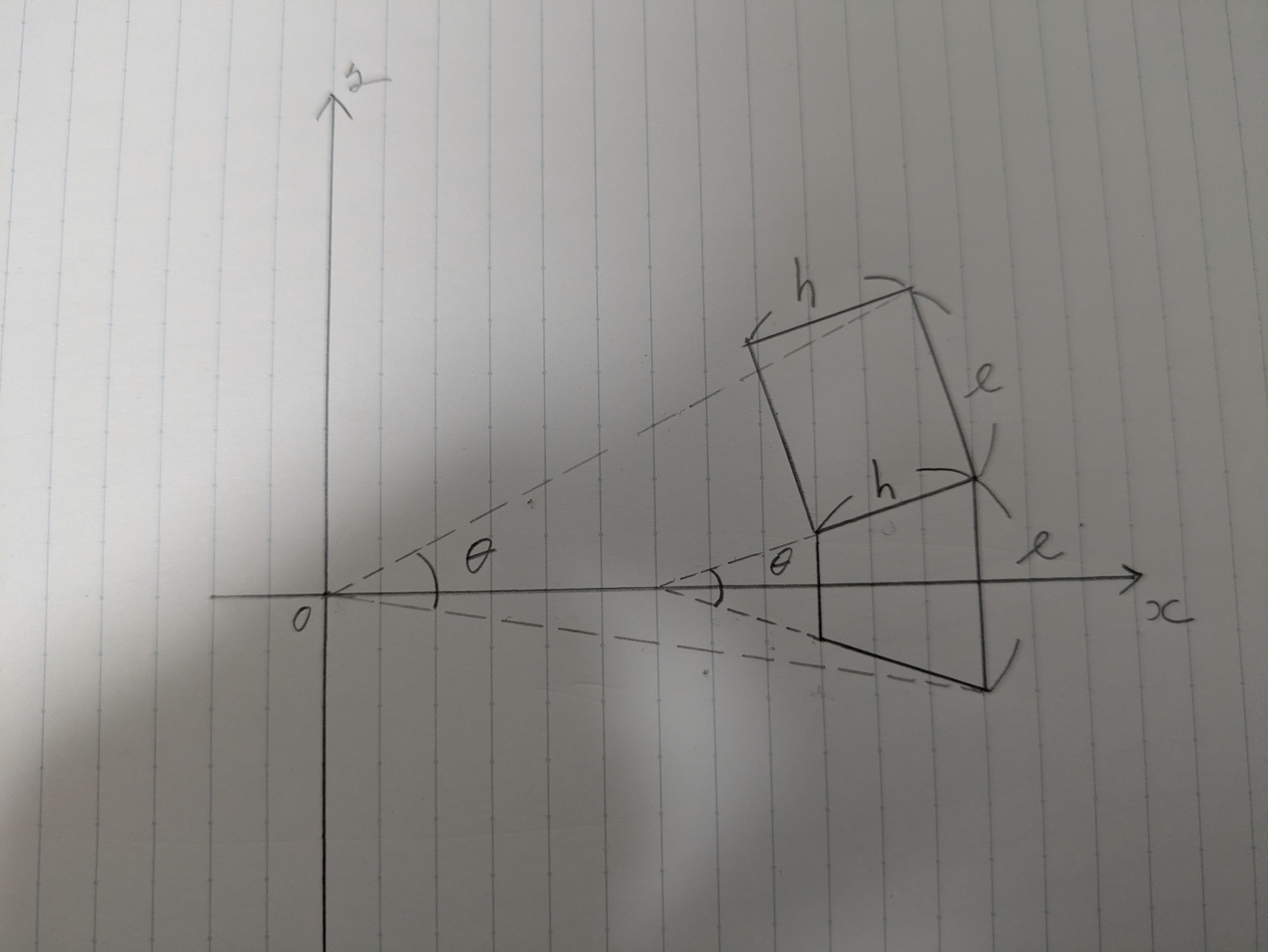
図の例:l, h, t, θ の対応(自作図に差し替えOK)
2. 写真のリング(台形配列)の作り方:数式
2-1. 台形の個数と離散条件
リング1周に台形が上面に \(n\) 個、下面に \(n\) 個現れるので台形総数は \(2n\)。 周方向にぐるっと閉じるため
\[ 2n\theta = 360^\circ \quad\Rightarrow\quad n = \frac{180^\circ}{\theta} \]
つまり \(\theta\) は \(360/(2n)\) の形でしか取れない(離散角)。
2-2. 外周半径 \(R_{\text{OUT}}\)
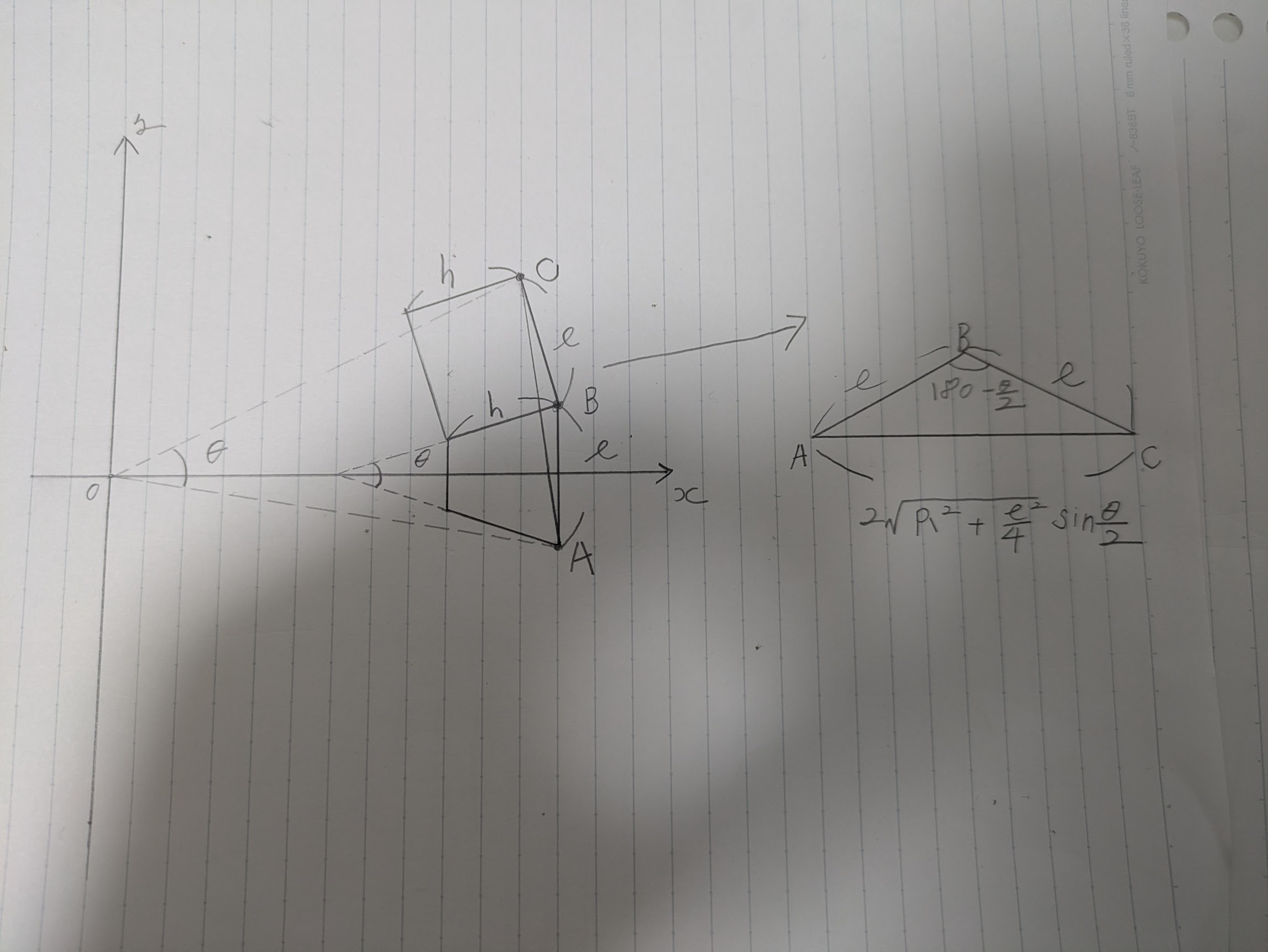
外周側セルが正六角形になる条件より、幾何学的な関係(余弦定理)から導出します。
▼導出式(余弦定理より)
▼途中式
▼結果 \(R\) (\(= R_{\text{OUT}}\))
※ \(\cos(180^\circ - \alpha) = -\cos\alpha\) などを利用してさらに整理できますが、導出過程としては上記のようになります。

2-3. 内周半径 \(R_{\text{IN}}\)
\[ R_{\text{IN}} = R_{\text{OUT}} - h\cos\frac{\theta}{2} \]
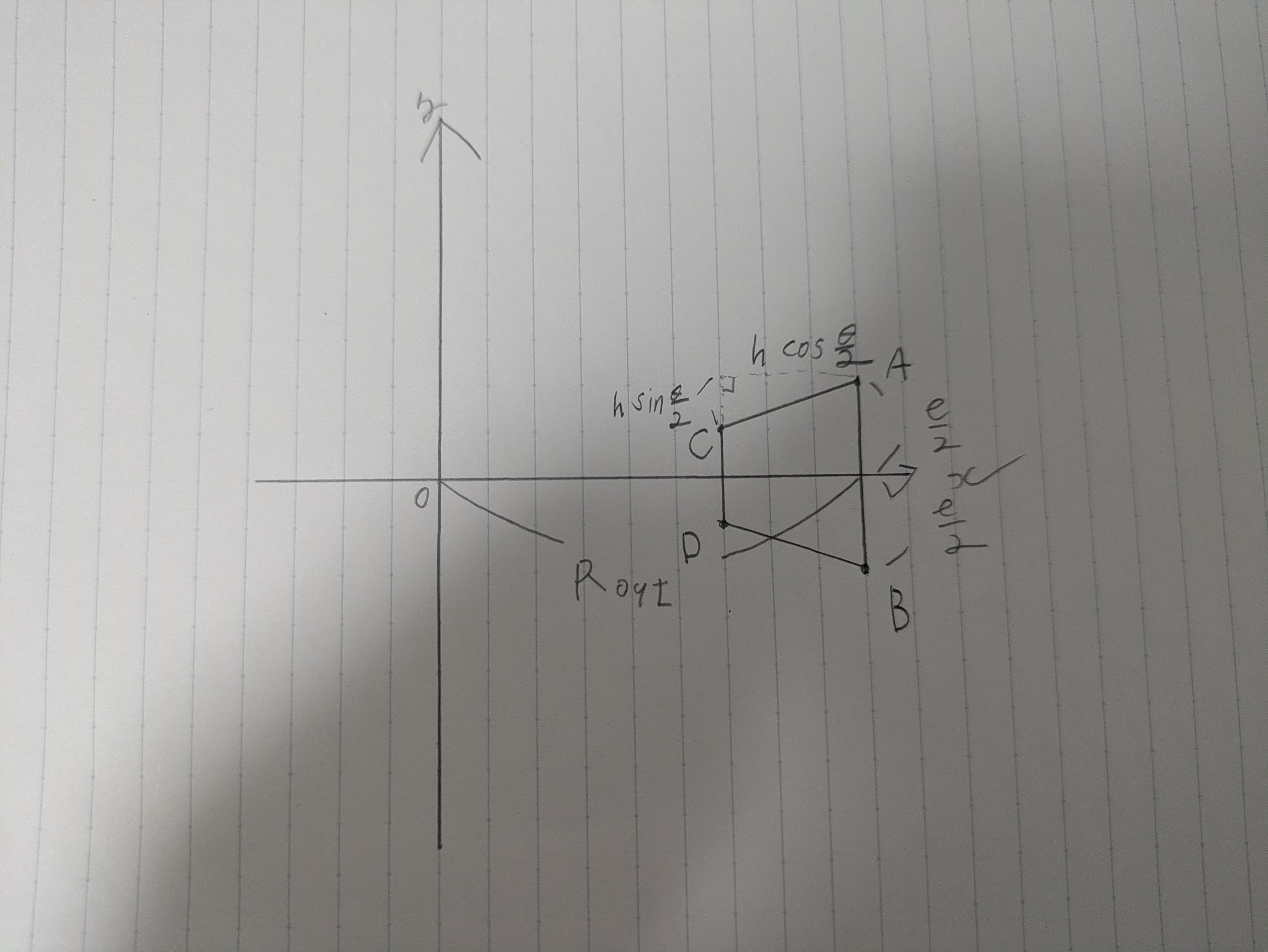
2-4. 1枚目の台形の4頂点
\[ A=(R_{\text{OUT}},+\tfrac{l}{2}),\quad B=(R_{\text{OUT}},-\tfrac{l}{2}) \] \[ C=\left(R_{\text{OUT}}-h\cos\tfrac{\theta}{2},\; \tfrac{l}{2}-h\sin\tfrac{\theta}{2}\right) \] \[ D=\left(R_{\text{OUT}}-h\cos\tfrac{\theta}{2},\; -\tfrac{l}{2}+h\sin\tfrac{\theta}{2}\right) \]
2-5. 回転コピーしてリング化
台形を回転行列 \(\mathbf{R}(\theta)\) を使って、角度 \(\theta\) ごとに \(2n\) 個配置します。 これにより円周方向に閉じたリング構造が形成されます。
\[ [A_i,B_i,C_i,D_i] =\mathbf{R}(\theta)^i[A,B,C,D]\quad (i=0,\dots,2n-1) \]
3. Webデモ:設計変数入力→図形生成
l, θ, h を変えると、円筒ハニカムの台形リング配置がリアルタイムに更新される。
4. 作り方(コルゲート法)
- リング状シートを設計 台形と斜面(平行四辺形)を交互に並べた展開図を作る。
- コルゲート状に折る 台形が上下面、斜面が側面に出るよう山折り谷折り。
- 2枚を接着してセル生成 台形面同士が向かい合うように貼ると六角形セルができる。
- 積層して高さhへ これを繰り返し円筒全体のコアを構成。

リング展開図 → 折り → 接着 → 積層
5. 設計のコツ
- θ が小さいほどセル数が増える(滑らかな円筒・細かいセル)。
- l を大きくすると軽くなるが剛性は下がる。
- h を下げたり Rout を大きくすると平板ハニカムに近づく。
6. 剛性の傾向(ざっくり)
外周側せん断剛性 \(G_{\text{OUT}}\) と内周側せん断剛性 \(G_{\text{IN}}\) は
Gout = ((Rout - h*cos(θ/2)) / Rout)^3 * Gin- l が大きいほど剛性は低下
- h が小さい/曲率が小さいほど平板ハニカム値へ収束
参考文献
本ページの理論・数式はこの論文を参考にしています。
-
https://doi.org/10.1299/transjsme.25-00002
日本機械学会論文集「円筒ハニカムコアの展開図設計と剛性評価」
